Равна полная площадь цилиндра. Примеры того, как вычислить площадь цилиндра

Найдите площадь осевого сечения, перпендикулярного основаниям цилиндра. Одна из сторон этого прямоугольника равна высоте цилиндра, вторая - диаметру окружности основания. Соответственно, площадь сечения в этом случае будет равна произведению сторон прямоугольника. S=2R*h, где S - площадь сечения, R – радиус окружности основания, заданный условиями задачи, а h - высота цилиндра, также заданная условиями задачи.

Если сечение перпендикулярно основаниям, но при этом не проходит через ось вращения, прямоугольника не будет равняться диаметру окружности. Ее нужно вычислить. Для этого в задачи должно быть сказано, на каком расстоянии от оси вращения проходит плоскость сечения. Для удобства вычислений постройте окружность основания цилиндра, проведите радиус и отложите на нем расстояние, на котором от центра окружности находится сечение. От этой точки проведите к перпендикуляры до их пересечения с окружностью. Соедините точки пересечения с центром. Вам нужно найти хорды. Найдите размер половины хорды по теореме Пифагора. Он будет равняться квадратному корню из разности квадратов радиуса окружности от центра до линии сечения. a2=R2-b2. Вся хорда будет, соответственно, равна 2а. Вычислите площадь сечения, которая равна произведению сторон прямоугольника, то есть S=2a*h.

Цилиндр можно рассечь , не проходящей через плоскости основания. Если поперечное сечение проходит перпендикулярно оси вращения, то оно будет представлять собой круг. Площадь его в этом случае равна площади оснований, то есть вычисляется по формуле S=πR2.

Полезный совет

Чтобы точнее представить себе сечение, сделайте чертеж и дополнительные построения к нему.

Источники:

• сечение цилиндра площадь

Линия пересечения поверхности с плоскостью принадлежит одновременно поверхности и секущей плоскости. Линия пересечения цилиндрической поверхности секущей плоскостью, параллельной прямой образующей – прямая линия. Если секущая плоскость перпендикулярна к оси поверхности вращения – в сечении будет окружность. В общем случае линия пересечения цилиндрической поверхности с секущей плоскостью – кривая линия.

Вам понадобится

• Карандаш, линейка, треугольник, лекала, циркуль, измеритель.

Инструкция

На фронтальной плоскости проекций П₂ линия сечения совпадает с проекцией секущей плоскости Σ₂ в виде прямой.
Обозначьте точки пересечения образующих цилиндра с проекцией Σ₂ 1₂, 2₂ и т.д. до точек 10₂ и 11₂.

На плоскости П₁ – это окружность. Отмеченные на плоскости сечения Σ₂ точки 1₂ , 2₂ и т.д. с помощью линии проекционной связи спроектируются на очерке этой окружности. Обозначьте их горизонтальные проекции симметрично относительно горизонтальной оси окружности.

Таким образом, проекции искомого сечения определены: на плоскости П₂ – прямая (точки 1₂, 2₂…10₂); на плоскости П₁ – окружность (точки 1₁, 2₁…10₁).

По двум постройте натуральную величину сечения данного цилиндра фронтально-проектирующей плоскостью Σ. Для этого используйте способ проекций.

Проведите плоскость П₄ параллельно проекции плоскости Σ₂. На этой новой оси x₂₄ отметьте точку 1₀. Расстояния между точками 1₂ – 2₂, 2₂ – 4₂ и т.д. с фронтальной проекции сечения отложите на оси x₂₄, проведите тонкие линии проекционной связи перпендикулярно оси x₂₄.

В данном способе плоскостью П₄ заменяется плоскость П₁, поэтому с горизонтальной проекции размеры от оси до точек перенесите на ось плоскости П₄.

Например, на П₁ для точек 2 и 3 это будет расстояние от 2₁ и 3₁ до оси(точка А) и т.д.

Отложив с горизонтальной проекции указанные расстояния, получите точки 2₀, 3₀, 6₀, 7₀, 10₀, 11₀. Затем для большей точности построения, определяются остальные, промежуточные, точки.

Соединив лекальной кривой все точки, получите искомую натуральную величину сечения цилиндра фронтально-проектирующей плоскостью.

Источники:

• как заменить плоскость

Совет 3: Как найти площадь осевого сечения усеченного конуса

Чтобы решить данную задачу, необходимо вспомнить, что такое усеченный конус и какими свойствами он обладает. Обязательно сделайте чертеж. Это позволит определить, какую геометрическую фигуру представляет собой сечение . Вполне возможно, что после этого решение задачи уже не будет представлять для вас сложности.

Инструкция

Круглый конус – тело, полученное путем вращения треугольника вокруг одного из его катетов. Прямые, исходящие из вершины конуса и пересекающие его основание, называются образующими. Если все образующие равны, то конус является прямым. В основании круглого конуса лежит круг. Перпендикуляр, опущенный на основание из вершины, является высотой конуса . У круглого прямого конуса высота совпадает с его осью. Ось – это прямая, соединяющая с центром основания. Если горизонтальная секущая плоскость кругового конуса , то его верхнее основание представляет собой круг.

Поскольку в условии задачи не оговорено, именно конус дается в данном случае, можно сделать вывод, что это прямой усеченный конус, горизонтальное сечение которого параллельно основанию. Его осевое сечение, т.е. вертикальная плоскость, которая через ось круглого конуса , представляет собой равнобочную трапецию. Все осевые сечения круглого прямого конуса равны между собой. Следовательно, чтобы найти площадь осевого сечения , требуется найти площадь трапеции, основаниями которой диаметры оснований усеченного конуса , а боковые стороны – его образующие. Высота усеченного конуса является одновременно высотой трапеции.

Площадь трапеции определяется по формуле:S = ½(a+b) h, где S – площадь трапеции;a – величина нижнего основания трапеции;b – величина ее верхнего основания;h – высота трапеции.

Поскольку в условии не оговорено, какие именно даны, можно , что диаметры обеих оснований усеченного конуса известны: AD = d1 – диаметр нижнего основания усеченного конуса ;BC = d2 – диаметр его верхнего основания; EH = h1 – высота конуса .Таким образом, площадь осевого сечения усеченного конуса определяется: S1 = ½ (d1+d2) h1

Источники:

• площадь усеченного конуса

Цилиндр является пространственной фигурой и состоит из двух равных оснований, которые представляют собой круги и боковой поверхности, соединяющей линии, ограничивающие основания. Чтобы вычислить площадь цилиндра , найдите площади всех его поверхностей и сложите их.

Площадь каждого основания цилиндра равна πr 2 , площадь обоих оснований составит 2πr 2 (рис.).

Площадь боковой поверхности цилиндра равна площади прямоугольника, основание которого равно 2πr , а высота равна высоте цилиндра h , т. е. 2πrh .

Полная поверхность цилиндра составит: 2πr 2 + 2πrh = 2πr (r + h ).

За площадь боковой поверхности цилиндра принимается площадь развертки его боковой поверхности.

Поэтому площадь боковой поверхности прямого кругового цилиндра равна площади соответствующего прямоугольника (рис.) и вычисляется по формуле

S б.ц. = 2πRH, (1)

Если к площади боковой поверхности цилиндра прибавить площади двух его оснований, то получим площадь полной поверхности цилиндра

S полн. =2πRH + 2πR 2 = 2πR (H + R).

Объем прямого цилиндра

Теорема. Объем прямого цилиндра равен произведению площади его основания на высоту , т. е.

где Q - площадь основания, а Н - высота цилиндра.

Так как площадь основания цилиндра равна Q, то существуют последовательности описанных и вписанных многоугольников с площадями Q n и Q’ n таких, что

\(\lim_{n \rightarrow \infty}\) Q n = \(\lim_{n \rightarrow \infty}\) Q’ n = Q.

Построим последовательности призм, основаниями которых являются рассмотренные выше описанные и вписанные многоугольники, а боковые ребра параллельны образующей данного цилиндра и имеют длину H. Эти призмы являются описанными и вписанными для данного цилиндра. Их объемы находятся по формулам

V n = Q n H и V’ n = Q’ n H.

Следовательно,

V= \(\lim_{n \rightarrow \infty}\) Q n H = \(\lim_{n \rightarrow \infty}\) Q’ n H = QH.

Следствие.
Объем прямого кругового цилиндра вычисляется по формуле

V = π R 2 H

где R - радиус основания, а H - высота цилиндра.

Так как основание кругового цилиндра есть круг радиуса R, то Q = π R 2 , и поэтому

При изучении стереометрии одной из главных тем становится «Цилиндр». Площадь боковой поверхности считается если не главной, то немаловажной формулой при решении геометрических задач. Однако важно помнить и определения, которые помогут сориентироваться в примерах и при доказательстве различных теорем.

Понятие цилиндра

Вначале нужно рассмотреть несколько определений. Только после их изучения можно приступать к рассмотрению вопроса о формуле площади боковой поверхности цилиндра. На основе этой записи можно вычислить и иные выражения.

• Под цилиндрической поверхностью понимают плоскость, описываемую образующей, движущейся и остающейся параллельной заданному направлению, скользящей по имеющейся кривой.
• Имеется и второе определение: цилиндрическую поверхность образуют множество параллельных прямых, пересекающих заданную кривую.
• Образующей называют условно высоту цилиндра. При ее перемещении вокруг оси, проходящей через центр основания, получается обозначенное геометрическое тело.
• Под осью подразумевают прямую, проходящую через оба основания фигуры.
• Цилиндром называется стереометрическое тело, ограниченное пересекающимися боковой поверхностью и 2 параллельными плоскостями.

Существуют разновидности данной объемной фигуры:

1. Под круговым подразумевают цилиндр, направляющая которого - это окружность. Его главными составляющими считаются радиус основания и образующая. Последняя равна высоте фигуры.
2. Существует прямой цилиндр. Свое название он получил благодаря перпендикулярности образующей к основаниям фигуры.
3. Третий вид - скошенный цилиндр. В учебниках можно встретить и другое его название «круговой цилиндр со скошенным основанием». Данную фигуру определяет радиус основания, минимальная и максимальная высоты.
4. Под равносторонним цилиндром понимают тело, имеющее равные между собой высоту и диаметр круглой плоскости.

Условные обозначения

Традиционно основные «компоненты» цилиндра принято называть следующим образом:

• Радиус основания - R (он же заменяет аналогичную величину стереометрической фигуры).
• Образующая - L.
• Высота - H.
• Площадь основания - S осн (иначе говоря, необходимо найти указанный параметр круга).
• Высоты скошенного цилиндра - h 1 ,h 2 (минимальная и максимальная).
• Площадь боковой поверхности - S бок (если ее развернуть, то получится своего рода прямоугольник).
• Объем стереометрической фигуры - V.
• Площадь полной поверхности - S.

«Компоненты» стереометрической фигуры

Когда изучается цилиндр, площадь боковой поверхности играет немаловажную роль. Связано это с тем, что данная формула входит в несколько других, более сложных. Поэтому необходимо быть хорошо подкованным в теории.

Основными составляющими фигуры являются:

1. Боковая поверхность. Как известно, она получается благодаря движению образующей по заданной кривой.
2. Полная поверхность включает в себя имеющиеся основания и боковую плоскость.
3. Сечением цилиндра, как правило, выступает прямоугольник, расположенный параллельно оси фигуры. Иначе его называют плоскостью. Оказывается, длина и ширина по совместительству являются составляющими других фигур. Так, условно длинами сечения являются образующие. Ширина - параллельные хорды стереометрической фигуры.
4. Под осевым сечением подразумевают расположение плоскости через центр тела.
5. И наконец, завершающее определение. Касательной называют плоскость, проходящую через образующую цилиндра и находящуюся под прямым углом к осевому сечению. При этом должно выполниться одно условие. Указанная образующая должна входить в плоскость осевого сечения.

Основные формулы для работы с цилиндром

Для того чтобы ответить на вопрос, как найти площадь поверхности цилиндра, необходимо изучить основные «компоненты» стереометрической фигуры и формулы их нахождения.

Данные формулы отличаются тем, что вначале даются выражения для скошенного цилиндра, а затем - для прямого.

Примеры с разобранным решением

Необходимо узнать площадь боковой поверхности цилиндра. Дана диагональ сечения AC = 8 см (причем оно является осевым). При соприкосновении с образующей получается < ACD = 30°

Решение. Поскольку известны величины диагонали и угла, то в таком случае:

• CD = AC*cos 30°.

Комментарий. Треугольник ACD, в конкретном примере, прямоугольный. Это означает, что частное от деления CD и AC = косинусу имеющегося угла. Значение тригонометрических функций можно найти в специальной таблице.

Аналогично, можно найти и значение AD:

• AD = AC*sin 30°

Теперь необходимо вычислить по следующей формулировке нужный результат: площадь боковой поверхности цилиндра равна удвоенному результату перемножения «пи», радиуса фигуры и ее высоты. Следует воспользоваться и другой формулой: площадью основания цилиндра. Она равняется результату перемножения «пи» на квадрат радиуса. И наконец, последняя формула: общая площадь поверхности. Она равна сумме предыдущих двух площадей.

Даны цилиндры. Их объем = 128*п см³. У какого из цилиндров наименьшая полная поверхность?

Решение. Для начала нужно воспользоваться формулами нахождения объема фигуры и ее высоты.

Поскольку площадь полной поверхности цилиндра известна из теории, необходимо применить ее формулу.

Если рассматривать полученную формулу в качестве функции площади цилиндра, то минимальный «показатель» будет достигнут в точке экстремума. Для получения последнего значения необходимо воспользоваться дифференцированием.

Формулы можно посмотреть в специальной таблице по нахождению производных. В дальнейшем найденный результат приравнивается к нулю и находится решение уравнения.

Ответ: S min будет достигнута при h = 1/32 см, R = 64 см.

Дана стереометрическая фигура - цилиндр и сечение. Последнее проведено таким образом, что располагается параллельно оси стереометрического тела. У цилиндра следующие параметры: ВК = 17 см, h = 15 см, R = 5 см. Необходимо найти расстояние между сечением и осью.

Поскольку под сечением цилиндра понимается ВСКМ, т. е. прямоугольник, то его сторона ВМ = h. Необходимо рассмотреть ВМК. Треугольник является прямоугольным. Исходя из этого утверждения, можно вывести верное предположение, что МК = ВС.

ВК² = ВМ² + МК²

МК² = ВК² - ВМ²

МК² = 17² - 15²

Отсюда можно сделать вывод, что МК = ВС = 8 см.

Следующий шаг - проведение сечения через основание фигуры. Необходимо рассмотреть получившуюся плоскость.

AD - диаметр стереометрической фигуры. Он параллелен сечению, упомянутому в условии задачи.

BC - прямая, расположенная на плоскости имеющегося прямоугольника.

ABCD - трапеция. В конкретном случае она считается равнобедренной, поскольку вокруг нее описана окружность.

Если найти высоту полученной трапеции, то можно получить ответ, поставленный в начале задачи. А именно: нахождение расстояния между осью и проведенным сечением.

Для этого необходимо найти величины AD и ОС.

Ответ: сечение располагается 3 см от оси.

Задачи на закрепление материала

Дан цилиндр. Площадь боковой поверхности используется в дальнейшем решении. Известны другие параметры. Площадь основания - Q, площадь осевого сечения - М. Необходимо найти S. Иными словами, полную площадь цилиндра.

Дан цилиндр. Площадь боковой поверхности необходимо найти в одном из шагов решения задачи. Известно, что высота = 4 см, радиус = 2 см. Необходимо найти полную площадь стереометрической фигуры.

Площадь поверхности цилиндра. В этой статье мы рассмотрим задания связанные с площадью поверхности . На блоге уже рассмотрены задания с таким телом вращения как конус. Цилиндр тоже относится к телам вращения. Что требуется и нужно знать о площади поверхности цилиндра? Давайте посмотрим на развёртку цилиндра:

Верхнее и нижнее основание это два равных круга:

Боковая поверхность это прямоугольник. При чём одна сторона этого прямоугольника равна высоте цилиндра, а другая длине окружности основания. Напомню, что длина окружности равна:

Итак, формула поверхности цилиндра:

*Учить эту формулу не нужно! Достаточно знать формулы площади круга и длины его окружности, тогда вы всегда сможете записать указанную формулу. Важно её понимание! Рассмотрим задачи:

Длина окружности основания цилиндра равна 3. Площадь боковой поверхности равна 6. Найдите высоту и площадь поверхности цилиндра (считайте, что число Пи равно 3,14 и результат округлите до десятых).

Площадь полной поверхности цилиндра:

Даны длина окружности основания и площадь боковой поверхности цилиндра. То есть, нам дана площадь прямоугольника и одна его сторона, требуется найти другую сторону (это есть высота цилиндра):

Требуется радиус и тогда мы сможем найти указанную площадь.

Длина окружности основания равна трём, тогда запишем:

Таким образом

Округляем до десятых, получаем 7,4.

Ответ: h = 2; S = 7,4

Площадь боковой поверхности цилиндра равна 72Пи, а диаметр основания - 9. Найдите высоту цилиндра.

Значит

Ответ: 8

Площадь боковой поверхности цилиндра равна 64Пи, а высота - 8 . Найдите диаметр основания.

Площадь боковой поверхности цилиндра находится по формуле:

Диаметр равен двум радиусам, значит:

Ответ: 8

27058. Радиус основания цилиндра равен 2, высота равна 3. Найдите площадь боковой поверхности цилиндра, деленную на Пи.

27133. Длина окружности основания цилиндра равна 3, высота равна 2. Найдите площадь боковой поверхности цилиндра.

Формула радиуса цилиндра:
где V - объем цилиндра, h - высота

Цилиндр - геометрическое тело, которое получается при вращении прямоугольника вокруг его стороны. Также, цилиндр представляет собой тело, ограниченное цилиндрической поверхностью и двумя параллельными плоскостями, пересекающими ее. Эта поверхность образуется при движении прямой параллельно самой себе. При этом выделенная точка прямой перемещается вдоль определенной плоской кривой (направляющая). Данная прямая называется образующей цилиндрической поверхности.
Формула радиуса цилиндра:
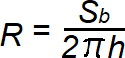
где Sb - площадь боковой поверхности, h - высота

Цилиндр - геометрическое тело, которое получается при вращении прямоугольника вокруг его стороны. Также, цилиндр представляет собой тело, ограниченное цилиндрической поверхностью и двумя параллельными плоскостями, пересекающими ее. Эта поверхность образуется при движении прямой параллельно самой себе. При этом выделенная точка прямой перемещается вдоль определенной плоской кривой (направляющая). Данная прямая называется образующей цилиндрической поверхности.
Формула радиуса цилиндра:
где S - площадь полной поверхности, h - высота